对于社交系统与电商网站,推荐系统占有很重要的位置,当数据量越来越大的时候,用户无法确定该选择什么商品,因此在电商系统中需要按照兴趣或者相似度给用户推荐相应的商品。相应的,在一个大型社交网络平台中,对于一些用户,我们希望推荐一些知名度较高,活跃度较高或者感兴趣的用户,比如一些明星,歌手,演员等等。在社交网络中,PageRank算法有着广泛的应用,因此,本篇文章主要介绍其原理。
对于大部分社交系统来说,如果只是简单的获取好友的信息远远不够,我们可以通过获取好友的好友的信息来扩展用户的朋友圈,使得信息量更加丰富,本项目中使用PageRank算法来完成二级邻居,然后按照Rank排序,选择Top5用户实现用户的好友的好友的推荐。
背景
PageRank算法设计之初就是应用于搜索引擎,从技术上看,搜索引擎需要解决以下三个问题:
- 建立资料库
- 建立一种数据结构,这种数据结构能通过keyword找到链接(文档)
- 对检索到的结果进行排序
建立资料库
本质就是一个爬虫问题,通过爬虫获取整个互联网的数据
索引
关键在于快速找到.
它的实现方式有: 倒排索引,签名文件,后缀树等。我们最熟悉的是倒排索引。(并不熟悉,以后有机会再看)
排序
排序是Google的搜索引擎能够兴起的一个决定性因素。
对网页排序有很多种方式,我们来看三种:
- 不评价
- 词频位置加权
- PageRank算法
不评价
就是原封不懂地把索引到的链接直接返回给用户,缺点就不说了,想找自己感兴趣的内容估计要费不少功夫。
词频位置加权
这种方式是一种只从关键词出现的次数和位置进行排序的方法。该方法以一个关键词与网页的相关度大小作为排序标准,而关键词在网页的相关度大小作为排序标准,而关键词在网页中的相关度则由它在网页中出现的频次和位置两方面加权计算得出。
缺点也很明显,容易出现刷分的情况,整篇文章中大量地刷关键词就能提高排名。
PageRank算法
真正找到计算网页自身质量的完美的数学模型是Google的创始人拉里佩奇和谢尔盖布林。 下一节讲一下原理。
PageRank算法原理
我们模拟一个悠闲的上网者,上网者首先随机选择一个网页打开,然后在这个网页上呆了几分钟后,跳转到该网页所指向的链接,这样无所事事、漫无目的地在网页上跳来跳去,PageRank就是估计这个悠闲的上网者分布在各个网页上的概率,这个概率就代表这个网页的重要性.
PageRank主要基于两个重要的假设:
- 如果一个网页被更多的网页链接到,说明这个网页更重要,也就是PageRank值会高
- 如果一个PageRank值高的网页链接到一个其他的网页,那么被链接到的网页的PageRank值会相应地因此而提高
如果一篇文章被越来越多的人引用,那么这篇文章可能就是一篇经典之作,如果这篇文章引用了其他的论文,那么一定程度上这篇被引用的文章也是一篇很好的文章。应用到社交网络中,如果一个好友被更多的人关注,那么说明该好友有很高的知名度和活跃度,那么,我们可以将该好友推荐给用户。
基于这两个假设,我们可以总结出PageRank算法的核心:
某个页面新的Rank值由当前所有页面的Rank值除以对应的出链个数再求和
如下图,可以更好的表达PageRank算法的思想:
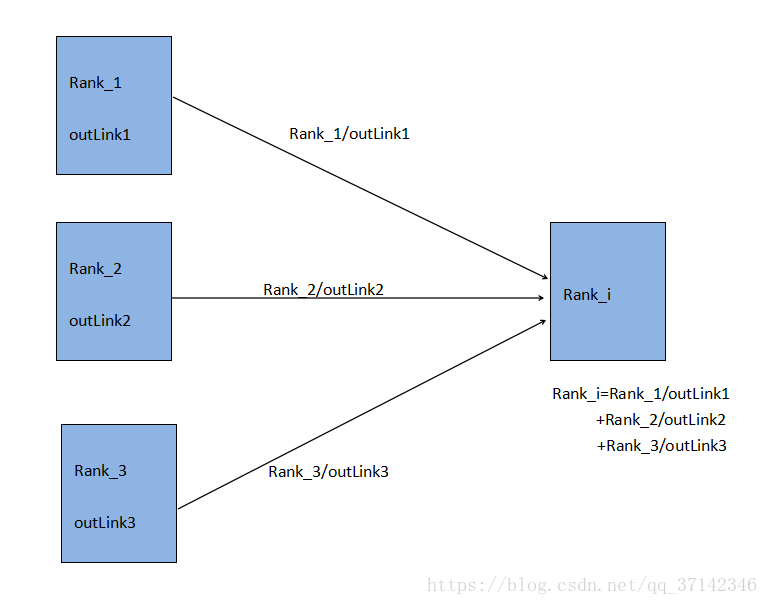
由上图可知,每个页面将自己的一部分rank传递给某个页面,我们可以通过计算传递给某个页面的所有rank值的和来计算出它的rank值,当然,不可能是通过一次计算完成,我们刚开始可以给每个页面赋予一个初始rank值,比如$\frac{1}{N}(N为页面总数)$,通过迭代计算得到该页面的rank值。
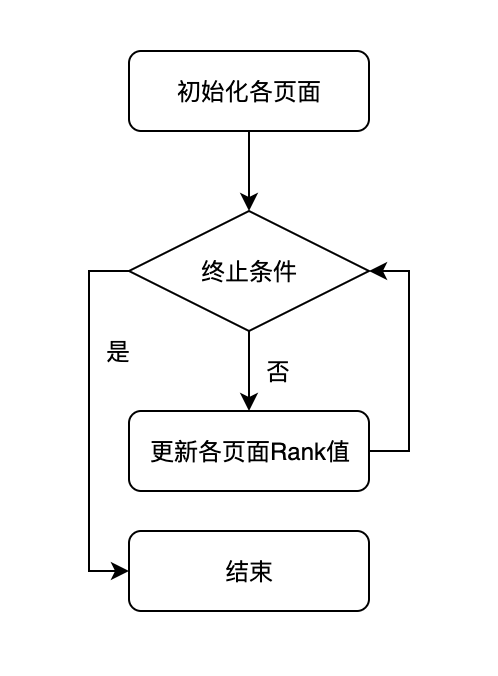
迭代计算停止的条件为:
- 新的所有页面的Rank值与旧的所有页面的Rank值之间的变化小于一个预先设定的值。(因为正常情况下变化是收敛的)
- 迭代计算的次数大于预先设定的值。
抽象模型
有向图
使用有向图表示:
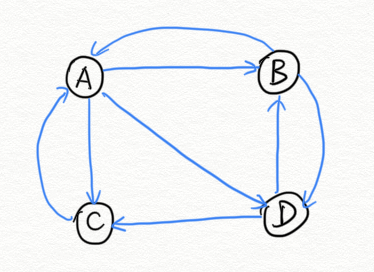
这个例子中只有四个网页,如果当前在A网页,那么悠闲的上网者将会各以1/3的概率跳转到B、C、D,这里的3表示A有3条出链,如果一个网页有k条出链,那么跳转任意一个出链上的概率是1/k,同理D到B、C的概率各为1/2,而B到C的概率为0。
转移矩阵
我们在做计算的时候会将该图表示成一个二维的矩阵,我们做一个转换,就会变成下图的矩阵形式。M(i,j)表示j节点指向i节点的概率 ,一般来说每列和为1。
生成的转移矩阵非常简单,矩阵的每一列代表该顶点所代表的页面除以对应页面的出链数得到的。
更新Rank值
有了转移矩阵,我们可以来定义行向量V,V的第i个分量记录$Page_i$对应的Rank值,因此一次Rank的更新可以表示为:
在算法的第一轮计算中,我们假设上网者在每一个网页的概率都是相等的,即1/n,于是初试的概率分布就是一个所有值都为1/n的n维列向量$V_0$,用$V_0$去右乘转移矩阵M,就得到了第一步之后上网者的概率分布向量$MV_0$,得到一个nX1的矩阵$V_1$,这个$V_1$一轮迭代计算出来的PageRank值。下面是$V_1$的计算过程:
得到了$V_1$后,再用$V_1$去右乘M得到$V_2$,一直下去,即$V_n=MV_{n-1}$,最终V会收敛.
不断的迭代,最终得到结果.
算法漏洞
但是在迭代计算中,我们需要考虑如下两大阻力: Dead End和Spider Trap:
Dead End
Dead End就是指一个页面只有入链但是没有出链,这时转移矩阵M的一列为零,导致最后结果为零。这时web不是强连通的,即存在某一类节点不指向别人,如下图的D。这个时候我们的算法就会出问题了,它不满足收敛性了。
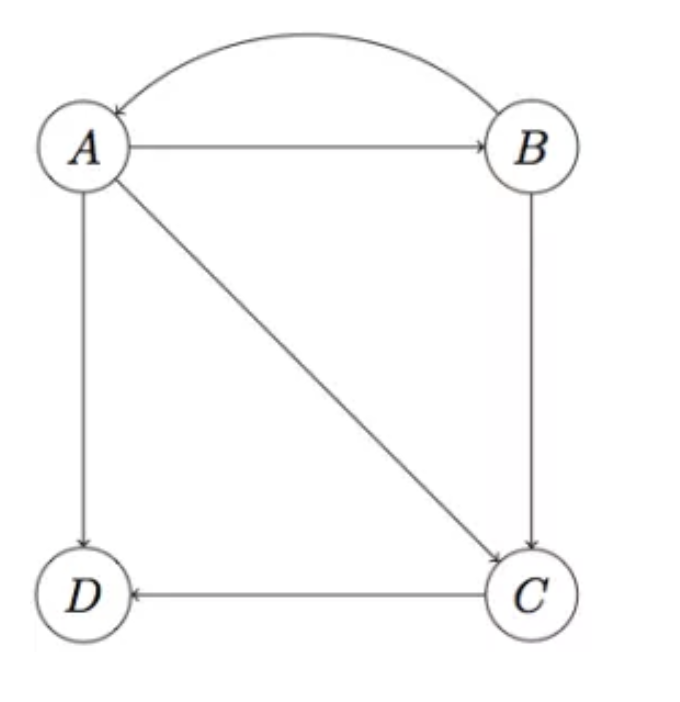
为什么不满足收敛性了?
我们上面描述的上网者的行为是一个其实马尔科夫过程)的实例,要满足收敛性,需要具备一个条件:图是强连通的,即从任意网页可以到达其他任意网页。一旦出现如上图的D的节点,就不满足收敛性的。
Spider Trap
Spider Trap指页面的所有出链都指向自己,这样会使迭代结果中只有自己的页面的Rank值很高。其他页面的Rank值为零。
模拟随机跳转
要克服上面两个问题,我们需要将迭代计算公式做如下转变。我们可以加入一个随机跳转机制.
即假设每个页面有很小概率拥有一个指向其他页面的链接。
在事实上,这是模拟上网者除了不断的点击网页上的链接来跳转之外,还有一定概率输入地址的方式、使用浏览器标签等来访问
表现出来就是:其他页面本来传递给一个页面的Rank值需要做一个折扣,作为补偿,可能需要一个页面指向该页面并且传递Rank值给该页面,该跳转的概率为β,因此表达式变为:
其中,N为页面总数;e为一个N维且各个分量都是1的向量;β通过经验得知一般设为0.15.
此时的计算结果过程为:
好友推荐实现思路
- 根据登陆者id获取所有好友的id(set1)
- 根据set1获取好友的好友的id(set2)
- 去除set2中的set1和登陆者id(set3)
- 对set3依照PageRank算法进行迭代
- 取迭代结果的topK(快排)

